Time-Invariant Finite State Machines

A friend posited a question about my previous finite state machines post: how do we model scheduled state transitions in a finite state machine? For example, with the door finite state machine, the door might close automatically after t seconds. Similarly, the button finite state machine might timeout if the user holds the button down for too long.

Scheduling the transition

Let's take the door example as we saw earlier, except modify it to automatically transition from open to closed after two seconds if it hasn't been closed.

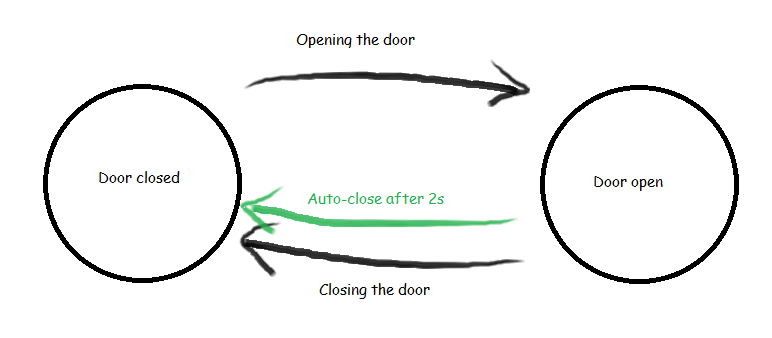
The original solution, with no auto-closing, has been copied below for reference.

type OpenState = "open";
type ClosedState = "closed";

type DoorState = OpenState | ClosedState;

function close(state: OpenState): ClosedState {
  return "closed";
}

function open(state: ClosedState): OpenState {
  return "open";
}

One approach to implementing an automatic door closing is to simply schedule a close action with setTimeout(). This works, but is both wildly unsatisfying and has some hidden complexity. Consider, for example, when the door is manually closed and then reopened. The existing timeout must be cancelled and rescheduled, otherwise the door may close prematurely. This might be implemented as such:

let door: DoorState = "closed";

door = open(door);
let timeout = setTimeout(() => door = close(door), 2000);
door = close(door);
clearTimeout(timeout);
door = open(door);
timeout = setTimeout(() => door = close(door), 2000);

Perhaps some of that logic can be abstracted to common functions, but as I mentioned, wildly unsatisfying. There is a better solution, which the title of this post hints at: making the finite state machine time-invariant.

What is time, even?

To make the finite state machine time-invariant, we incorporate the time that the last event occurred into the state. Then, in order to determine if the door is open or not, instead of looking directly at the state, we compute the output state based on the door state and the time of the last event.

If that's a bit confusing, don't worry. It's a bit simpler to understand with code. First, we adjust our OpenState to include the time that it was opened at. The ClosedState doesn't need to change because the door doesn't auto-open, but we adjust the signature a bit to keep things consistent.

type OpenState = { type: "open", at: Date };
type ClosedState = { type: "closed" };

In these signatures, type is a string constant.

Our DoorState remains unchanged

type DoorState = OpenState | ClosedState;

The transition for close doesn't change, but now open must include the date to correctly satisfy the type definition.

function close(state: OpenState): ClosedState {
  return { type: "closed" };
}

function open(state: ClosedState): OpenState {
  return { type: "open", at: new Date() };
}

Now, in order to determine if the door is open or closed, we need a view function.

function view(state: DoorState): "open" | "closed" {
  switch (state.type) {
    case "closed":
      return "closed";
    case "open":
      const now = new Date();
      if (now.getTime() - state.at.getTime() > 2 * 1000) {
        // The door has been opened for more then 2s, so it's really closed.
        return "closed";
      } else {
        return "open";
      }
  }
}

And now, we can properly open our door and expect that it transitions out of being opened after two seconds.

let door: DoorState = { type: "closed" };

door = open(door);  // Open the door.

console.log(view(door));                          // Prints open.
setTimeout(() => console.log(view(door)), 2100);  // Prints closed, 2100 to avoid a race.

Try this on the TypeScript playground.

Lenses: a tinted view of the state

Perhaps you'd like to tell me now: Kevin, this is cheating! The state isn't actually transitioned!

It's true that the underlying state isn't actually transitioned, but the key insight here is that the output of view is uniquely determined by the input state (door) and current time. In fact, all modelable systems will behave like this. Unless another transition occurs, any closed machine that follows like the one above can be deterministically modeled by its initial state and time.

This is a pretty nice property, as it suggests that as long as we incorporate the time of the event into our state, we can project our state however we like. Even as the finite state machine gets more complex, as long as we do not introduce any non-determinism, the output state can always be calculated as a function of the last known state. In fact, because computer random number generators are often not truly random, we can even model "randomness" too, to a degree.

The best reference to this approach of using a view function that I could find is the functional lens. The view function above only implements a getter, however it's also possible to implement a setter. I don't think it matches exactly, but I think the name works: the lens is a view of the state. In this case, the view that we actually want.

Extending beyond time

Considering the above approach more deeply, we can also extend further by lifting any details that might result in "scheduled transitions" into the current state. For example, if the door must automatically close and open repeatedly but manually opening or closing it resets the process, we can also model this by incorporating the time into the closed state.

Here's an exercise I'll leave to the reader: suppose the door will auto-close after two seconds unless the door was opened within one second of the last close. How might we model this scenario without actually invoking the transition?

Take a stab at it on the TypeScript playground, some example test cases are provided.

Comment on this post on Twitter