Finite state machines are a powerful, but underutilized model for computation. They are the most flexible and "perfect" abstraction of how practical code behaves that I've run across, even moreso than my love of everything-is-a-function. There are more flexible models, such as Turing machines, but finite state machines strike a balance between being overly abstract and being grounded in application.
A finite state machine is a machine that transitions between states, of which there are finitely many.
We'll take this example straight from Wikipedia. A door has two states: open and closed. Transitioning between them is simply opening a closed door or closing an open door.
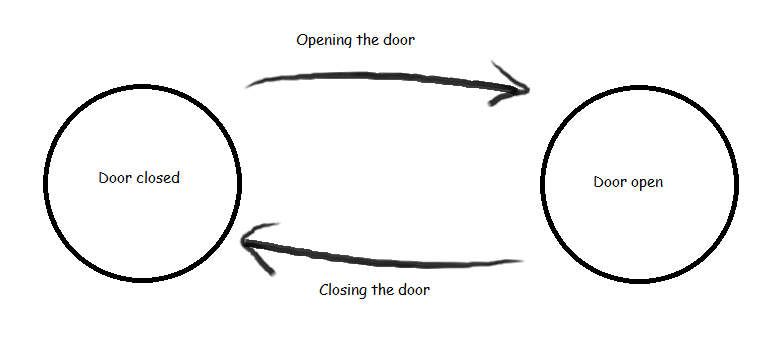
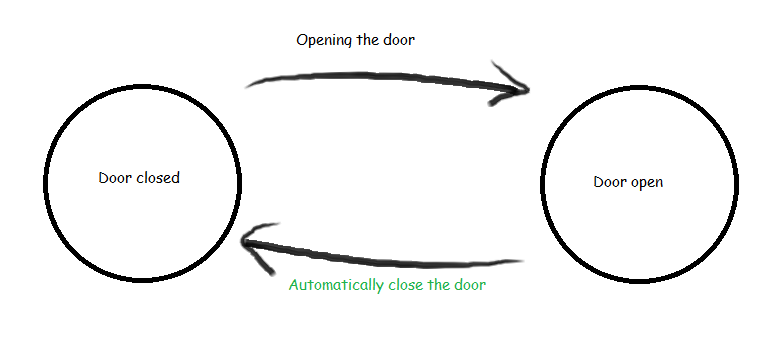
With these states and transitions, the door can be modeled as a finite state machine. In this example, we don't dictate what opens or closes the door, but we can also specify that too. For example, in an automatically closing door the closing action is simply labeled as an automatic transition.
Now that we have a door, let's implement it. Some tutorials choose to use a library like XState, but I think finite state machines can be implemented more elegantly without any libraries. Moreover, bare-bones implementations get to the real power of such models.
First, declare our states. Each state is represented by a
type.
type OpenState = "open"; type ClosedState = "closed"; type DoorState = OpenState | ClosedState;
Second, declare our transitions. Each transition is represented by a
function.
function close(state: OpenState): ClosedState {
return "closed";
}
function open(state: ClosedState): OpenState {
return "open";
}
And that's it! To use this implementation, we can maintain our door as a
variable.
let door: DoorState = "open"; door = close(door); // Close the door. door = open(door); // Open it again. door = open(door); // This won't compile, can't open an open door.
Try this on the TypeScript playground.
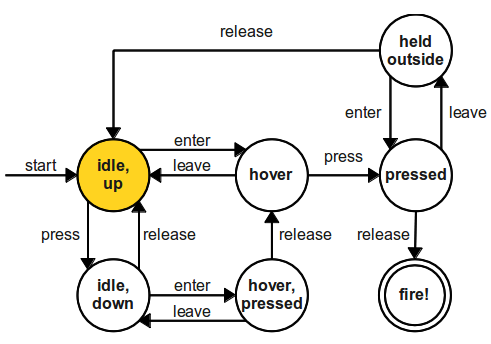
The door example is simple, however. Practical finite state machines have many more states, transitions, and behaviors. But these can still be modeled with the above pattern. Let's consider an HTML button, which can be modeled with the following diagram.

Play around with the behavior here, taking note of how the transitions work.
Using the above framework, first declare our states.
type IdleUpState = "idle, up"; type IdleDownState = "idle, down"; type HoverState = "hover"; type HoverPressedState = "hover, pressed"; type HeldOutsideState = "held outside"; type PressedState = "pressed"; type FireState = "fire!"; type ButtonState = | IdleUpState | IdleDownState | HoverState | HoverPressedState | HeldOutsideState | PressedState | FireState;
Then declare our transitions. I've omitted leave,
press, and release to keep this readable.
function enter(state: IdleUpState | IdleDownState | HeldOutsideState): ButtonState {
switch (state) {
case "idle, up":
return "hover";
case "idle, down":
return "hover, pressed";
case "held, outside":
return "pressed";
}
}
...
Unfortunately, when we try using this implementation, something goes wrong!
let button: ButtonState = "idle, up"; button = enter(button); // This is ok. button = leave(button); // This won't compile, but should.
What happened here? Sadly, the compiler doesn't know that
button is a valid state when it gets passed to
leave. There are three ways to solve this problem:
#1 results in a lot of boilerplate but will work and #3 is outside the scope of this post, so I'll focus on #2. In order to not transition if the state is invalid, we adjust the transition so nothing happens if an incorrect state is passed in.
function enter(state: ButtonState): ButtonState {
switch (state) {
case "idle, up":
return "hover";
case "idle, down":
return "hover, pressed";
case "held, outside":
return "pressed";
default:
return state;
}
}
And with that simple change, our code now works.
let button = "idle, up"; button = enter(button); // This is ok. button = leave(button); // Also now works.
Lastly, we want to bind our transitions to events.
let state = "idle, up";
button.on("mouseenter", () => state = enter(state));
button.on("mouseleave", () => state = enter(state));
document.on("mousedown", () => state = press(state));
document.on("mouseup", () => state = release(state));
And we're done! state now tracks the state of the button
following the behavior of the state machine. Try it below, view the source
with your browser.

Another approach to solving #2 would be to use a higher order function
called a reducer. This would remove the need for default
statements, and might look something like this.
type EnterAction = "enter";
type LeaveAction = "leave";
type PressAction = "press";
type ReleaseAction = "release";
type Action =
| EnterAction
| LeaveAction
| PressAction
| ReleaseAction;
function reducer(action: Action, state: ButtonState): ButtonState {
switch(action) {
case "enter": {
if (state === "idle, up" || state === "idle, down" || state === "held, outside") {
return enter(state);
}
return state;
}
...
}
}
The other cases have been omitted for brevity, but if you're familiar with the direction that frontend development has been going for the last few years, this might seem incredibly familiar. This is no surprise: finite state machines are an incredibly good model for applications. UI development in general has captured a lot of this intuition by decoupling state representation from rendering.
If we take a step back and look again at the button finite state machine as an example, suppose we only look at the subset of states in the red box.
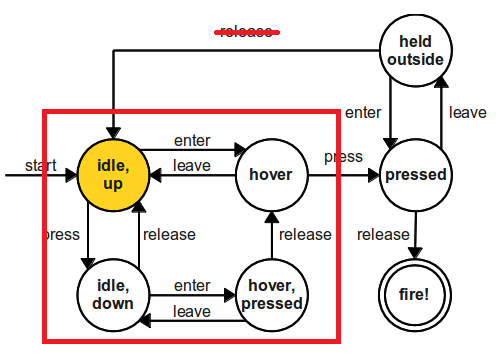
This is still a finite state machine! In fact, finite state machines are
composed of finite state machines. And when we look at the
implementation of reducer, it looks suspiciously similar to
the code for a transition, because it is, in fact, a transition.
So finite state machines are just composed of finite state machines. Take this to an extreme and look at a computer. A von Neumann architected computer is composed of memory, which stores state, and a processor, which performs transitions. Therefore, a physical computer is nothing but a finite state machine. Functions are nothing but transitions between memory states. And I think this realization is why writing a finite state machine from scratch is so insightful, because viewing code as nothing but state transitions offers a way to dramatically reduce complexity and make code easier to understand.
Finite state machines aren't just good models for computing, they are an exceptionally good model for practical software engineering. The next time you run into a complex problem and it's hard to rack your head around the complexity, try decomposing it into simple states and transitions between them. As we've seen, finite state machines are composed of finite state machines, so not only can you start by modeling a small subset of states and build up from there, but also every problem is guaranteed to be modelable.
After all, if it runs on a computer, it runs on a finite state machine, so it has to be, fundamentally, a transition between states. That is, in my opinion, unreasonably effective.
Want more finite state machines? Read on with Time-Invariant Finite State Machines!
Comment on this post on Twitter or Hacker News