Note: I'm not a professional behavioral economist. If you find any mistakes, insights, or suggestions, please email me. I'd love to learn from you!
Let's play a game. Send exactly 0.1 ETH (~$37 today) to the following address and if the transaction id ends with an odd digit (50% chance), I'll send 0.2 ETH back.
0x3730B5054AC8DDdbC672a831f7ff2f2ba501038b
This is a manual process, but I will send winners 0.2 ETH within 24h.
Most people won't play even though the expected value of playing is zero (minus transaction fees). Because humans are naturally loss averse: we tend to prefer avoiding losses to equivalent gains. If you don't want to play because you don't trust me, funnily enough, this is also characterized by loss aversion. When we incur losses, our amygdala triggers a negative emotional response, but the equivalent positive response doesn't happen for gains. In fact, our biological response causes us to feel losses around 2-3 times worse than the equivalent gains and insurance companies work by trading on that difference.
To model the preference to avoid losses, our utility curve, the intrinsic value of a specific loss/gain, follows
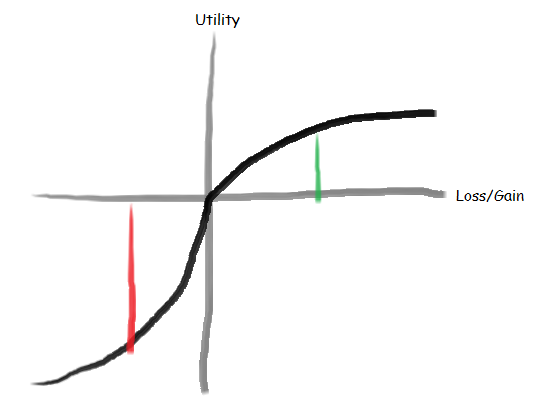
Specifically, we value losses much more negatively than the equivalent gain. This asymmetry is known as loss aversion. Someone who is not loss averse has a utility curve that is symmetric with a red and green line approximately the same size.
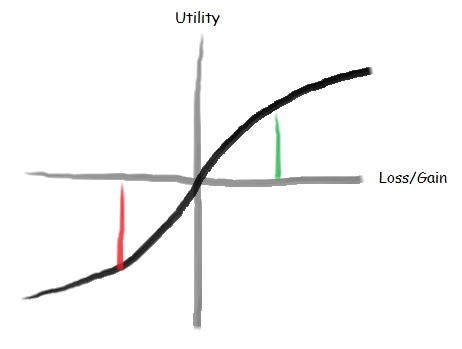
Despite loss aversion being tied to core human behavior, most economists do not consider it to be rational.
Under rational behavior $1 is worth $1 and $100 is worth $100. Saving $100 is functionally equivalent to making $100. Corporations operate under this strategy, observing that cost savings are equivalent to gained profit.
The difference between a rational actor and a human behavior suggests that there is a market opportunity available. Consider a game with the following two choices.
For the same loss aversion reason, many players will choose option 1: the idea of losing $1000 is harder to stomach than just incurring a $550 loss. Perfectly rational actors, however, will choose option 2 because its expected loss is $500.
This $50 difference is known as the risk premium.
Taking calculated risks can look scary because the apparent expected payoff appears far more negative than the true expected payoff. Think about the prospect of quitting your job, asking your crush out, or going skydiving. In all of these cases, odds are that everything will work out, but the perceived fear can be high.
But in all these cases, we don't have the luxury of choosing the outcome and reality doesn't always go according to plan.
Whatever comes, we will help you quickly and easily. mobiliar.ch
So, reality might stick us with choice 2: a 50% chance of $1000 loss and a 50% chance of $0 loss.
Now, an insurance company comes and observes that the true expected value is different from the perceived expected value and that it can collect this risk premium by selling an insurance product.
By aggregating over all consumers, as long as the insurance company is able to estimate the true expected value, it can sell a lower-risk, guaranteed-loss product at above the perceived expected value and profit from the risk premium. So that's where insurance comes from: it insures me against unrecoverable loss by removing uncertainty.
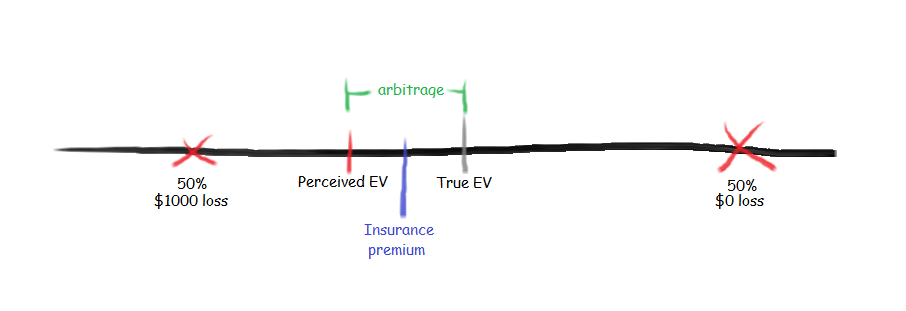
Consumers are willing to buy this product because they still stand to gain between the perceived expected value and the insurance premium. Specifically, the space between the insurance premium and the true expected value is the insurance company's profit and the space between the perceived expected value and the insurance premium is the consumer's profit.
The insurance companies are effectively trading risk as an product.
Interestingly, not every loss-aversion-affected game can be traded via risk reduction. When the option to not play is available, games with negative perceived expected value cannot be insured against. Take, for example, the double-or-nothing game offered in the introduction. The perceived expected value of playing the game is negative and the true expected value is zero. Because you are offered the option to also not play, however, any insurance policy that can arbitrage this difference would be dominated by the option to not play.
Therefore, artificial insurance policies also compete with certain natural mitigation strategies. Additional, non-market-taking solutions include putting agents in non-competitive environments or reducing the amount of information that is exposed. There are many other strategies and this area of behavioral economics is still actively researched, but the key takeaway is that converting these arbitrage opportunities to other forms of value (eg money) is not always as easy as selling an insurance product.
Of particular interest to me is how these relate to aligning agents' incentives, which I will talk about in a part two not-yet-published blog post. As a sneak peak, I view a scheme that adjusting the risk profile curve to match the linear curve of a business as a form of incentive alignment.
On a personal level, the existence of insurance and the loss aversion asymmetry has taught me that when I'm afraid of something, odds are that it's not rational. Usually, the true payoff curve is not aligned with what I'm afraid of. Sometimes, that helps make it easier to take risks but in other words, failing is not always as bad as it seems.
Put simply, I try to take some risks for the sake of taking them. Being a bit riskier usually will mean I'm closer to risk-neutral than risk-taking after factoring in my biases. That's how I capitalize on my personal risk arbitrage and collect my own risk premium without insurance.
For more cute die Mobiliar advertisements, visit their site (German)
Comment on this post on Twitter